How To Measure Modulus Of Elasticity

Posted on

An elastic modulus (also known as modulus of elasticity) is a quantity that measures an object or substance's resistance to being deformed elastically (i.e., non-permanently) when a stress is applied to it. The elastic modulus of an object is defined as the slope of its stress–strain curve in the elastic deformation region:[1] A stiffer material will have a higher elastic modulus. An elastic modulus has the form:

Multiply the value of F by the value of L1; then divide that quantity by the product of A times L2. The resulting value of these calculations is the elastic modulus of the material. Sims 4 hair mods not working. Elastic modulus values range from about 1,500 psi (pounds per square inch) for rubber to about 175 million psi for diamond. Modulus of Elasticity or 'Young's Modulus' is a measurement of the rate of change of strain as a function of stress. With respect to tensile testing, it may be referred to as Tensile Modulus. It represents the slope of the linear portion of a stress-strain curve. An elastic modulus (also known as modulus of elasticity) is a quantity that measures an object or substance's resistance to being deformed elastically (i.e., non-permanently) when a stress is applied to it. The elastic modulus of an object is defined as the slope of its stress–strain curve in the elastic deformation region: A stiffer material will have a higher elastic modulus.

λ=defstressstrain{displaystyle lambda {stackrel {text{def}}{=}} {frac {text{stress}}{text{strain}}}}

where stress is the force causing the deformation divided by the area to which the force is applied and strain is the ratio of the change in some parameter caused by the deformation to the original value of the parameter. If stress is measured in pascals, then since strain is a dimensionless quantity, the units of λ will be pascals as well.[2]

Specifying how stress and strain are to be measured, including directions, allows for many types of elastic moduli to be defined. The three primary ones are:

  1. Young's modulus (E) describes tensile elasticity, or the tendency of an object to deform along an axis when opposing forces are applied along that axis; it is defined as the ratio of tensile stress to tensile strain. It is often referred to simply as the elastic modulus.
  2. The shear modulus or modulus of rigidity (G or μ{displaystyle mu ,}) describes an object's tendency to shear (the deformation of shape at constant volume) when acted upon by opposing forces; it is defined as shear stress over shear strain. The shear modulus is part of the derivation of viscosity.
  3. The bulk modulus (K) describes volumetric elasticity, or the tendency of an object to deform in all directions when uniformly loaded in all directions; it is defined as volumetric stress over volumetric strain, and is the inverse of compressibility. The bulk modulus is an extension of Young's modulus to three dimensions.
How To Measure Modulus Of ElasticityHow To Measure Modulus Of Elasticity

Three other elastic moduli are Poisson's ratio, Lamé's first parameter, and P-wave modulus.

Homogeneous and isotropic (similar in all directions) materials (solids) have their (linear) elastic properties fully described by two elastic moduli, and one may choose any pair. Given a pair of elastic moduli, all other elastic moduli can be calculated according to formulas in the table below at the end of page.

Inviscid fluids are special in that they cannot support shear stress, meaning that the shear modulus is always zero. This also implies that Young's modulus for this group is always zero.

In some English texts the here described quantity is called elastic constant, while the inverse quantity is referred to as elastic modulus.

See also[edit]

References[edit]

  1. ^Askeland, Donald R.; Phulé, Pradeep P. (2006). The science and engineering of materials (5th ed.). Cengage Learning. p. 198. ISBN978-0-534-55396-8.
  2. ^Beer, Ferdinand P.; Johnston, E. Russell; Dewolf, John; Mazurek, David (2009). Mechanics of Materials. McGraw Hill. p. 56. ISBN978-0-07-015389-9.

Further reading[edit]

  • Hartsuijker, C.; Welleman, J. W. (2001). Engineering Mechanics. Volume 2. Springer. ISBN978-1-4020-4123-5.

Modulus Of Resilience

  • De Jong, Maarten; Chen, Wei (2015). 'Charting the complete elastic properties of inorganic crystalline compounds'. Scientific Data. 2: 150009. Bibcode:2013NatSD..2E0009D. doi:10.1038/sdata.2015.9. PMC4432655.
Conversion formulae
Homogeneous isotropic linear elastic materials have their elastic properties uniquely determined by any two moduli among these; thus, given any two, any other of the elastic moduli can be calculated according to these formulas.
K={displaystyle K=,}E={displaystyle E=,}λ={displaystyle lambda =,}G={displaystyle G=,}ν={displaystyle nu =,}M={displaystyle M=,}Notes
(K,E){displaystyle (K,E)}3K(3K−E)9K−E{displaystyle {tfrac {3K(3K-E)}{9K-E}}}3KE9K−E{displaystyle {tfrac {3KE}{9K-E}}}3K−E6K{displaystyle {tfrac {3K-E}{6K}}}3K(3K+E)9K−E{displaystyle {tfrac {3K(3K+E)}{9K-E}}}
(K,λ){displaystyle (K,lambda )}9K(K−λ)3K−λ{displaystyle {tfrac {9K(K-lambda )}{3K-lambda }}}3(K−λ)2{displaystyle {tfrac {3(K-lambda )}{2}}}λ3K−λ{displaystyle {tfrac {lambda }{3K-lambda }}}3K−2λ{displaystyle 3K-2lambda ,}
(K,G){displaystyle (K,G)}9KG3K+G{displaystyle {tfrac {9KG}{3K+G}}}K−2G3{displaystyle K-{tfrac {2G}{3}}}3K−2G2(3K+G){displaystyle {tfrac {3K-2G}{2(3K+G)}}}K+4G3{displaystyle K+{tfrac {4G}{3}}}
(K,ν){displaystyle (K,nu )}3K(1−2ν){displaystyle 3K(1-2nu ),}3Kν1+ν{displaystyle {tfrac {3Knu }{1+nu }}}3K(1−2ν)2(1+ν){displaystyle {tfrac {3K(1-2nu )}{2(1+nu )}}}3K(1−ν)1+ν{displaystyle {tfrac {3K(1-nu )}{1+nu }}}
(K,M){displaystyle (K,M)}9K(M−K)3K+M{displaystyle {tfrac {9K(M-K)}{3K+M}}}3K−M2{displaystyle {tfrac {3K-M}{2}}}3(M−K)4{displaystyle {tfrac {3(M-K)}{4}}}3K−M3K+M{displaystyle {tfrac {3K-M}{3K+M}}}
(E,λ){displaystyle (E,lambda )}E+3λ+R6{displaystyle {tfrac {E+3lambda +R}{6}}}E−3λ+R4{displaystyle {tfrac {E-3lambda +R}{4}}}2λE+λ+R{displaystyle {tfrac {2lambda }{E+lambda +R}}}E−λ+R2{displaystyle {tfrac {E-lambda +R}{2}}}R=E2+9λ2+2Eλ{displaystyle R={sqrt {E^{2}+9lambda ^{2}+2Elambda }}}
(E,G){displaystyle (E,G)}EG3(3G−E){displaystyle {tfrac {EG}{3(3G-E)}}}G(E−2G)3G−E{displaystyle {tfrac {G(E-2G)}{3G-E}}}E2G−1{displaystyle {tfrac {E}{2G}}-1}G(4G−E)3G−E{displaystyle {tfrac {G(4G-E)}{3G-E}}}
(E,ν){displaystyle (E,nu )}E3(1−2ν){displaystyle {tfrac {E}{3(1-2nu )}}}Eν(1+ν)(1−2ν){displaystyle {tfrac {Enu }{(1+nu )(1-2nu )}}}E2(1+ν){displaystyle {tfrac {E}{2(1+nu )}}}E(1−ν)(1+ν)(1−2ν){displaystyle {tfrac {E(1-nu )}{(1+nu )(1-2nu )}}}
(E,M){displaystyle (E,M)}3M−E+S6{displaystyle {tfrac {3M-E+S}{6}}}M−E+S4{displaystyle {tfrac {M-E+S}{4}}}3M+E−S8{displaystyle {tfrac {3M+E-S}{8}}}E−M+S4M{displaystyle {tfrac {E-M+S}{4M}}}S=±E2+9M2−10EM{displaystyle S=pm {sqrt {E^{2}+9M^{2}-10EM}}}

There are two valid solutions.
The plus sign leads to ν≥0{displaystyle nu geq 0}.

The minus sign leads to ν≤0{displaystyle nu leq 0}.
(λ,G){displaystyle (lambda ,G)}λ+2G3{displaystyle lambda +{tfrac {2G}{3}}}G(3λ+2G)λ+G{displaystyle {tfrac {G(3lambda +2G)}{lambda +G}}}λ2(λ+G){displaystyle {tfrac {lambda }{2(lambda +G)}}}λ+2G{displaystyle lambda +2G,}
(λ,ν){displaystyle (lambda ,nu )}λ(1+ν)3ν{displaystyle {tfrac {lambda (1+nu )}{3nu }}}λ(1+ν)(1−2ν)ν{displaystyle {tfrac {lambda (1+nu )(1-2nu )}{nu }}}λ(1−2ν)2ν{displaystyle {tfrac {lambda (1-2nu )}{2nu }}}λ(1−ν)ν{displaystyle {tfrac {lambda (1-nu )}{nu }}}Cannot be used when ν=0⇔λ=0{displaystyle nu =0Leftrightarrow lambda =0}
(λ,M){displaystyle (lambda ,M)}M+2λ3{displaystyle {tfrac {M+2lambda }{3}}}(M−λ)(M+2λ)M+λ{displaystyle {tfrac {(M-lambda )(M+2lambda )}{M+lambda }}}M−λ2{displaystyle {tfrac {M-lambda }{2}}}λM+λ{displaystyle {tfrac {lambda }{M+lambda }}}
(G,ν){displaystyle (G,nu )}2G(1+ν)3(1−2ν){displaystyle {tfrac {2G(1+nu )}{3(1-2nu )}}}2G(1+ν){displaystyle 2G(1+nu ),}2Gν1−2ν{displaystyle {tfrac {2Gnu }{1-2nu }}}2G(1−ν)1−2ν{displaystyle {tfrac {2G(1-nu )}{1-2nu }}}
(G,M){displaystyle (G,M)}M−4G3{displaystyle M-{tfrac {4G}{3}}}G(3M−4G)M−G{displaystyle {tfrac {G(3M-4G)}{M-G}}}M−2G{displaystyle M-2G,}M−2G2M−2G{displaystyle {tfrac {M-2G}{2M-2G}}}
(ν,M){displaystyle (nu ,M)}M(1+ν)3(1−ν){displaystyle {tfrac {M(1+nu )}{3(1-nu )}}}M(1+ν)(1−2ν)1−ν{displaystyle {tfrac {M(1+nu )(1-2nu )}{1-nu }}}Mν1−ν{displaystyle {tfrac {Mnu }{1-nu }}}M(1−2ν)2(1−ν){displaystyle {tfrac {M(1-2nu )}{2(1-nu )}}}
Retrieved from 'https://en.wikipedia.org/w/index.php?title=Elastic_modulus&oldid=904868026'

The modulus of elasticity describes the relationship between the stress applied to a material and its corresponding strain. Stress is defined as a force applied over a unit area, with typical units of pounds per square inch (psi) or Newtons per square meter — also known as pascals (Pa). Strain is a measure of the amount that a material deforms when stress is applied and is calculated by measuring the amount of deformation when under stress, as compared to the matter's original dimensions. Modulus of elasticity is based on Hooke’s Law of elasticity and can be calculated by dividing the stress by the strain.

Steel

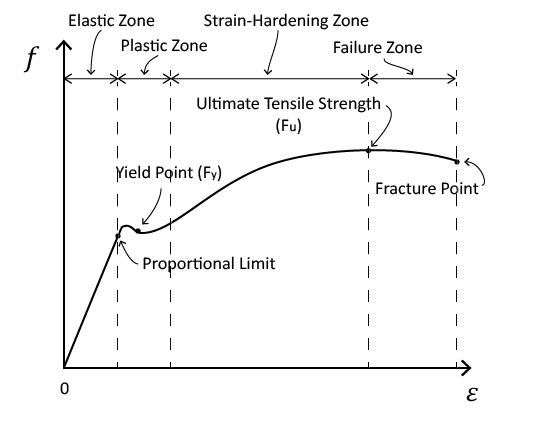
How To Measure Modulus Of Elasticity Graph

For many materials at low levels of stress and under tension, the stress and strain are proportional — meaning they increase and decrease in a constant way, relative to each other. Deformation of a material that occurs when the stress and strain behave proportionally is known as elastic deformation or elastic strain. Modulus of elasticity describes the relationship between stress and strain when under these conditions.

Young's Modulus Of Wood

Elasticity is the ability of a material to return to its original state or dimensions after a load, or stress, is removed. Elastic strain is reversible, meaning the strain will disappear after the stress is removed and the material will return to its original state. Materials that are exposed to intense levels of stress may deform to the point where the stress and strain no longer behave proportionally, and the material will not return to its original dimensions. This is referred to as plastic deformation or plastic strain.